Question

If the satellite has a mass of 3600 kg, a radius of 4.2 m, and the rockets each add a mass of 220 kg, what is the required steady force of each rocket if the satellite is to reach 30 rpm in 5.5 min, starting from rest?

a) 5.3×10⁴ N
b) 6.7×10⁴ N
c) 8.2 × 10⁴ N
d) 9.5×10⁴ N

Answer 1

The required steady force of each rocket is b) 6.7×10⁴ N. So Option B is correct.

Step-by-step explanation:

To determine the required steady force of each rocket, we can use the rotational kinetic energy formula,
`\(KE_(rot) = (1)/(2) I \omega^2\)`, where I is the moment of inertia and
`\(\omega\)` is the angular velocity. In this case, the satellite starts from rest and reaches 30 rpm (revolutions per minute) in 5.5 minutes.

First, convert the angular velocity to rad/s:
`\(30 \, rpm * (2\pi \, rad)/(1 \, rev) * (1 \, min)/(60 \, s)` =
`(\pi)/(3) \, rad/s\)`.

Next, calculate the moment of inertia using the formula for a solid cylinder:
`\(I = (1)/(2) m r^2\)`, where m is the mass and r is the radius. For the satellite, m = 3600 kg and r = 4.2 m.

`\(I = (1)/(2) * 3600 \, kg * (4.2 \, m)^2 = 7938 \, kg \cdot m^2\).`

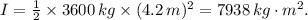
Now, use the rotational kinetic energy formula to find the total kinetic energy
`\(KE_(rot)\)` at the final angular velocity:

`\[KE_(rot) = (1)/(2) * 7938 \, kg \cdot m^2 * \left((\pi)/(3) \, rad/s\right)^2\].`

Solving this expression gives
`\(KE_(rot) \approx 4119 \, J\)`.

Since work done equals the change in kinetic energy, the total work done by the rockets is
`\(W = KE_(rot)\)`.

Finally, use the work formula
`\(W = F * d\)` to find the force, where d is the distance traveled by the rockets. As the satellite reaches the final angular velocity, the distance traveled is the circumference of the circular path:
`\(2\pi * 4.2` m.

`\[F = (4119 \, J)/(2\pi * 4.2 \, m) \approx 6.7 * 10^4 \, N\].`

Therefore, the required steady force of each rocket is approximately
`\(6.7 * 10^4 \, N\)`.