Question

Rich also has £400 pounds invest 3% compound interest . How many years does he need to invest the money to get at least £475

Answer 1

Answer: 6 years

Explanation:

Formula to calculate compound amount:
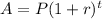`A=P(1+r)^t`, where P= Principal , r=rate of interest, t= time

Given: P = £400, r = 3% = 0.03 , A= 475

Required equation:
`400(1+0.03)^t\geq475`

`400(1.03)^t\geq475\\\\\Rightarrow\ (1.03)^t\geq(475)/(400)\\\\\Rightarrow\ (1.03)^t\geq1.1875`

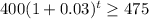
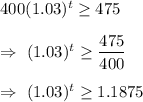
Taking log on both sides , we get

`t \log 1.03\geq\log1.1875\\\\\Rightarrow\ t(0.0128372)\geq(0.0746336)\\\\\Rightarrow\ t\geq(0.0746336)/(0.0128372)=5.81385\approx6`

Hence, he needs to invest the money for 6 years to get atleast £475.