Question

If a spinner is divided into 5 equal pieces and labeled with numbers one to five inclusive, what is the probability of landing on an odd-numbered piece exactly 6 times in 20 spins?

a) 0.037
b) 0.052
c) 0.067
d) 0.082

Answer 1

The probability of landing on an odd-numbered piece exactly 6 times in 20 spins is calculated using the binomial probability formula, with a probability of success on a single trial being 3/5.

Step-by-step explanation:

The problem is asking us to calculate the probability of landing on an odd-numbered piece exactly 6 times in 20 spins of a spinner divided into 5 equal pieces and numbered one to five. This is a binomial probability problem where we need to identify the number of successes (landing on an odd number), the number of trials (spins), and the probability of success on a single trial.

There are three odd numbers (1, 3, and 5) on the spinner, so the probability of landing on an odd number in one spin is 3/5. The probability of landing on an even number (2 or 4) would therefore be 2/5. Since we want exactly 6 successes (odd numbers) in 20 spins, we can use the binomial probability formula:

`\(P(X = k) = \binom{n}{k} * p^k * (1-p)^(n-k)\)`

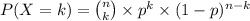
Where:

• n is the number of trials (spins), which is 20
• k is the number of successful trials (6)
• p is the probability of success on a single trial (3/5)
• 1-p is the probability of failure on a single trial (2/5)

Substituting the values into the formula gives us:

`\(P(X = 6) = \binom{20}{6} * \left((3)/(5)\right)^6 * \left((2)/(5)\right)^(14)\)`

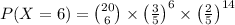
Calculating this probability will give us the answer to the question.