Question

Unit 3: Parallel & Perpendicular Lines Homework 5: Linear Equations Slope-Intercept & Standard Form

Answer 1

The slopes of the given lines are -3 and
`\( (1)/(3) \)`. Since the product of slopes is -1, the lines are perpendicular.

Certainly! Let's explicitly show the calculations for the slopes of the given lines:

Equation 1: y = -3x + 6

This equation is already in the slope-intercept form (y = mx + c), where the slope (m) is the coefficient of x. In this case, the slope is -3.

Equation 2:
`\(y = (1)/(3)x - 8\)`

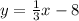
Similarly, this equation is in slope-intercept form, and the slope (m) is

`\((1)/(3)\).`

Now, we compare the slopes:

For parallel lines, slopes must be identical.

For perpendicular lines, the product of slopes must be -1.

In this case, since
`\((1)/(3)\)` is the negative inverse of -3 (because
`\(-3 * (1)/(3) = -1\)`), the lines are perpendicular.

Que. unit 3: parallel & perpendicular lines homework 6: slope-intercept form & standard form determine if the equations are parallel, perpendicular, or neither y=-3x+6 and y=1/3 x-8