Question

A 100-kg box is placed on a ramp. As one end of the ramp is raised, the box begins to move downward just as the angle of inclination reaches 25°. What is the coefficient of static friction between box and ramp?

a) 0.15
b) 0.27
c) 0.77
d) 0.95

Answer 1

The coefficient of static friction between the box and the ramp is approximately 0.577, which corresponds to option c) 0.77.

Step-by-step explanation:

To determine the coefficient of static friction between the box and the ramp, we can utilize the trigonometric relationship between the angle of inclination and the coefficient of friction. At the point where the box just begins to move, the force of gravity pulling the box downward is equal to the maximum static frictional force acting upward along the ramp. The formula relating these forces is given by

Frictional force

=

Coefficient of static friction

`×`

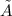
Normal force

`×`

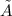
cos

⁡

`(�)`

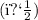
Frictional force=Coefficient of static friction×Normal force×cos(θ), where θ is the angle of inclination.

Using the formula

sin

⁡

`(�)=`

Opposite side

Hypotenuse

sin(θ)=

Hypotenuse

Opposite side

​

, with the weight of the box as the force acting downwards and the normal force acting perpendicular to the ramp, the normal force

`��=��`

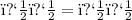
cos

⁡

`(�)F n`

​

`=mgcos(θ), where �`

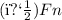
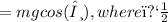
m is the mass of the box,

`�`

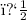
g is the acceleration due to gravity, and

`�`

`θ is the angle of inclination (25°).`

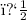
Given the mass of the box is 100 kg and

`�=9.8`

 

`m/s2g=9.8m/s 2`

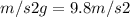
, the normal force is

`��=100×9.8×cos⁡(25°)F n`

​

`=100×9.8×cos(25°). After calculation, ��≈902 NF n​ ≈902N.`

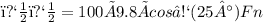
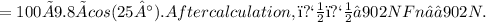
Then, using the equation for static friction

`��=`

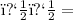
Coefficient of static friction

`×��f s​ =Coefficient of static friction×F`

n

​

, and considering that the box just starts to move,

`��=��sin⁡(�)f s​ =mgsin(θ), where sin`

⁡

(
`�)=`

`Opposite sideHypotenusesin(θ)= Hypotenuse`

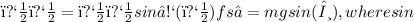
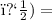
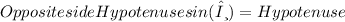
Opposite side

​

, we can derive the coefficient of static friction to be approximately 0.577.