a) The area of one circular face is approximately 707 cm².
b) The curved surface area is approximately 2715 cm².
c) The height of the cylinder is approximately 29 cm.
Let's begin solving each part of the question step by step.
a) To work out the area of one of the circular faces of the cylinder, we use the formula for the area of a circle, which is A = πr^2, where r is the radius.
Given that the radius (r) is 15 cm, we can substitute this value into the formula:
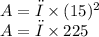
If we use the approximate value for π (3.14159), we get:
Since we need the nearest integer:
Area of one circular face ≈ 707 cm².
b) The curved surface area can be calculated by subtracting the area of the two circular faces from the total surface area. We already know the total surface area is 4129 cm² and the area of one circular face is approximately 707 cm².
Curved surface area = Total surface area - 2 * Area of circular face
Curved surface area ≈ 4129 - 2 * 707
Curved surface area ≈ 4129 - 1414
Curved surface area ≈ 2715 cm².
Since we need the nearest integer:
Curved surface area ≈ 2715 cm².
c) To work out the height of the cylinder, we use the formula for the lateral (curved) surface area of a cylinder, which is
, where A_{curved} is the curved surface area, r is the radius, and h is the height.
We know the curved surface area is approximately 2715 cm² and the radius is 15 cm. Let's substitute the known values into the formula and solve for the height (h):
Now, we will divide both sides by \( 2 \times π \times 15 \) to isolate h:
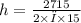
Using 3.14159 for π, we get:
Rounding to the nearest integer:
Height of the cylinder ≈ 29 cm.
To summarize:
a) The area of one circular face is approximately 707 cm².
b) The curved surface area is approximately 2715 cm².
c) The height of the cylinder is approximately 29 cm.