Question

Please help me solve this problem!

Answer 1

(a) A function that models the surface area A of the box in terms of the length of one side of the base x is
`A(x)=x^(2) +4xh`.

(b) The box dimensions that minimize the amount of material used are;

side length = 2.71 feet.

height = 1.36 feet.

In Mathematics and Geometry, the volume of a square prism can be calculated by using the following formula:

Volume of a square prism =
`x^(2)` × h

Volume of a square prism =
`x^(2)h`

where:

• x represents the length of a square prism.
• h represents the height of a square prism.

Part a.

In this context, the surface area (A) of the box in terms of the length of one side of the base x can be written as follows;

A(x) =
`x^(2)` + 4xh

Part b.

Since the volume of the box is 10 square feet, its height is given by;

Volume of a square prism =
`x^(2)h`

10 =
`x^(2)h`

`h=\frac{{10} }{x^(2) }`

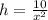
By substituting the value of h into the surface area function, we have;

A(x) =
`x^(2)` + 4xh

`A(x) = x^(2) + 4x((10 )/(x^(2)))\\\\A(x) = x^(2) + ((40 )/(x))`

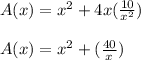
By taking the first derivative and equating to zero, we have;

`A'(x) = 2x - (40)/(x^(2) ) \\\\0= 2x - (40)/(x^(2) ) \\\\2x =(40)/(x^(2))\\\\2x^3=40\\\\x^3=20\\\\x=\sqrt[3]{20}`

x = 2.71 feet.

For the value of h, we have;

`h=\frac{{10} }{x^(2) }\\\\h=\frac{{10} }{2.71^(2) }`

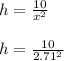
h = 1.36 feet.