Answer:
Compound future value = $23,300.59
Interest= $ 6,000.59
Explanation:
The compound future value (FV) can be calculated using the compound interest formula:
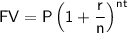
where:
-
 is the principal amount (initial investment),
is the principal amount (initial investment),
-
 is the annual interest rate (in decimal form),
is the annual interest rate (in decimal form),
-
 is the number of times interest is compounded per year,
is the number of times interest is compounded per year,
-
 is the time the money is invested for in years.
is the time the money is invested for in years.
In this case:
-
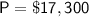
-
 (6% in decimal form)
(6% in decimal form)
-
 (compounded quarterly)
(compounded quarterly)
-
 years
years
First, calculate the compound future value (
 ):
):
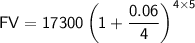
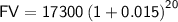

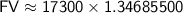
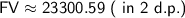
So, the compound future value (
 ) after 5 years is approximately $23,300.59.
) after 5 years is approximately $23,300.59.
Now, to find the interest earned, subtract the principal from the future value:
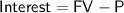
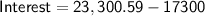
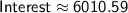
Therefore, the interest earned after 5 years is approximately $6,000.59.