A rectangular prism is 11 feet long and 5 feet wide. Its volume is 275 cubic feet. What is the height of the rectangular prism?

Question

asked Sep 21, 2024 79.2k views

2 Answers

Dr Herbie · Answer 1 · 2024-09-22T07:44:22+0000

Explanation:

the volume of such a prism is

length × width × height

therefore, based on what we are given :

275 = 11 × 5 × height = 55 × height

height = 275 / 55 = 5 ft

Max Doumit · Answer 2 · 2024-09-25T21:10:31+0000

Answer:

$\sf \textsf{height} = 5 ft$

Explanation:

The volume (
$\sf V$ ) of a rectangular prism is given by the formula:

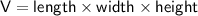
$\sf V = \textsf{length} * \textsf{width} * \textsf{height}$

In this case, we're given the (
$\sf \textsf{length} = 11$ ), the (
$\sf \textsf{width} = 5$ ), and the volume (
$\sf V = 275$ ).

Substitute in these values into the formula and solve for the height (
$\sf \textsf{height}$ ):

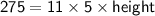
$\sf 275 = 11 * 5 * \textsf{height}$

First, find the product of 11 and 5:

$\sf 275 = 55 * \textsf{height}$

Now, solve for
$\sf \textsf{height}$ by dividing both sides of the equation by 55:

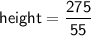
$\sf \textsf{height} = (275)/(55)$

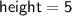
$\sf \textsf{height} = 5$

Therefore, the height of the rectangular prism is 5 feet.