Question

Graph the following Equation:

y+4=3/2(x-1)
C
a
€
E
-2 -1
5-
3+
2+
-1
-2+
WN
-3+
-4
1
2
3
4

Answer 1

A graph of the linear equation y + 4= 3/2(x - 1) is shown in the image attached below.

In Mathematics and Euclidean Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):

`y - y_1 = m(x - x_1)`

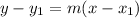
Where:

• x and y represent the data points.
• m represent the slope or rate of change.

Based on the information provided about the graph of this line, we can reasonably infer and logically deduce that a linear equation that models it can be written as follows;

`y - y_1 = m(x - x_1)`

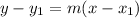
y + 4= 3/2(x - 1)

Since the given linear equation y + 4= 3/2(x - 1) is in point-slope form, we would start by plotting the y-intercept:

y + 4= 3/2(0 - 1)

y = -3/2 - 4

y = -11/2

Next, we would use an online graphing tool to plot the given linear equation for the values in its domain by starting with its y-intercept and moving 5.5 units up, followed by a horizontal shift to the right as shown in the graph attached below.