Question

A solution contains 7% salt. How much water should be added to 30 ounces of this solution to make a 5% solution?

Answer 1

12 ounces of water.

Explanation:

1. Set the initial values.

Total mass of the solution: 30 ounces.

Total mass of salt (solute): (30*0.07)= 2.1 ounces.

Total mass of water (solvent): (30*0.93) 27.9 ounces.

2. Find an equation that relates amount of water and percentage of salt.

Since we know that the amount of salt is 2.1 ounces, and it has to remain constant, we have to create a function such that the variable is the amount of water and it gives us the percentage of solution we are looking for. The function should look like this:

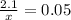`(2.1)/(x) =0.05`; where x is the mass of the water in the solution.

Side note: The number "0.05" is 5% converted into a decimal.

3. Solve the equation for x.

`(2.1)/(x) =0.05\\ \\(x)/(2.1) =(1)/(0.05) \\ \\x=(2.1)/(0.05) \\ \\x=42`

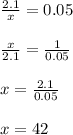
42 would be the total amount of ounces the solution should have in order to be a 5% solution. Therefore, 12 ounces (42-30) have to be added.

4. Conclude.

12 ounces of water have to be added to this solution in order to make it a 5% solution, where 2.1 ounces is salt and 39.9 is water.