Question

Given the equation A=250(1.1)t, you can determine that the interest is compounded annually and the interest rate is 10%. Suppose the interest rate were to change to being compounded quarterly. Rewrite the equation to find the new interest rate that would keep A and P the same.

What is the approximate new interest rate?

Convert your answer to a percentage, round it to the nearest tenth, and enter it in the space provided, like this: 42.53%

Answer 1

The new interest rate is about 0.1038.

As a percent, this is about 10.4%.

Explanation:

We are given:

`\displaystyle A=250(1.1)^t`

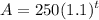
From this, we can determine that the interest rate is compounded annually at 10%.

We want a new equation that keeps A and P but the interest rate is compounded quarterly.

Compound interest is given by:

`\displaystyle A=P(1+(r)/(n))^(nt)`

Since we are compounding quarterly, n = 4. Since the rate is 10%, r = 0.1. P stays at 250. Therefore:

`\displaystyle A=250(1+(0.1)/(4))^(4t)`

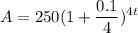
Add:

`\displaystyle A=250(1.025)^(4t)`

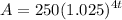
Rewrite:

`A=250((1.025)^4)^t`

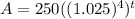
So:

`A\approx 250(1.1038)^t`

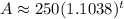
Therefore, the approximate new interest rate is 1.1038 - 1 or about 0.1038.

As a percent, this will be 0.1038 or about 10.4%.