Question

In an experimental grassland plot, researchers planted 20 seeds of a wildflower species that exhibits exponential growth with an intrinsic growth rate of 0.60. Approximate the maximum population size after 10 years.

Options:
A) 20×e ^0.6×10
B) 20×e^6×10
C) 20×e ^0.6
D) 20×e^ 6

Answer 1

The maximum population size after 10 years, following exponential growth, would be 20 seeds multiplied by e raised to the power of 0.6 times 10, which is reflected by Option
`A: 20×e^0.6×10.`

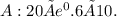
Step-by-step explanation:

When calculating the population size after a given time under exponential growth, we use the formula N(t) = N0ert, where N(t) is the future population size, N0 is the initial population size, e is the base of the natural logarithm, r is the intrinsic growth rate, and t is time. In your case, you started with 20 seeds and an intrinsic growth rate of 0.60. To find the population size after 10 years, you would substitute 20 for N0, 0.60 for r, and 10 for t in the formula.

Therefore, the maximum population size after 10 years would be calculated as 20×e0.6×10, which corresponds to Option A. Note that while populations can grow exponentially when resources are unlimited, they will often exhibit logistic growth as they approach the carrying capacity of their environment, eventually becoming stable.