This problem, we can use the conservation of energy principle. The potential energy lost by the falling weight is converted into the kinetic energy of both the falling weight and the rotating cylinder.
Let's denote:
 : mass of the falling weight (1.50 kg)
: mass of the falling weight (1.50 kg)
 : mass of the cylinder (3.25 kg)
: mass of the cylinder (3.25 kg)
R : radius of the cylinder (0.25 m, half of the diameter)
h : distance the weight falls
g : acceleration due to gravity
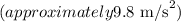
The potential energy lost by the falling weight is converted into the kinetic energy of both the falling weight and the rotating cylinder:
![\[ m_1gh = (1)/(2) m_1v^2 + (1)/(2) I\omega^2 \]](https://img.qammunity.org/2024/formulas/physics/college/v554y3ia8imouzd4itl98q75ajdl0eb4x5.png)
Where:
 is the speed of the falling weight (2.10 m/s)
is the speed of the falling weight (2.10 m/s)
 is the moment of inertia of the cylinder about its central axis
is the moment of inertia of the cylinder about its central axis
 is the angular velocity of the cylinder
is the angular velocity of the cylinder
The moment of inertia
 for a solid cylinder about its central axis is
for a solid cylinder about its central axis is
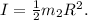
Now, let's substitute the values and solve for
 and
and
 :
:
![\[ 1.50 \cdot 9.8 \cdot h = (1)/(2) \cdot 1.50 \cdot (2.10)^2 + (1)/(2) \cdot (1)/(2) \cdot 3.25 \cdot (0.25)^2 \cdot \omega^2 \]](https://img.qammunity.org/2024/formulas/physics/college/iqyycrgkn60rashuraed2zpat6l3936n1a.png)
Solving for
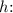
![\[ 14.7h = 1.575 + 0.1015625\omega^2 \]](https://img.qammunity.org/2024/formulas/physics/college/8zqzujzsb0i2wld1apkdj0fnqqgdfuyfsc.png)
Now, we need to find
 . The linear velocity of a point on the rim of the cylinder is given by
. The linear velocity of a point on the rim of the cylinder is given by
 . Since
. Since
 is also the velocity of the falling weight, we have:
is also the velocity of the falling weight, we have:
![\[ 2.10 = 0.25\omega \]](https://img.qammunity.org/2024/formulas/physics/college/gtcoum6on13w5r6uu43x94fl769jpn5h1m.png)
Solving for

![\[ \omega = (2.10)/(0.25) = 8.4 \ \text{rad/s} \]](https://img.qammunity.org/2024/formulas/physics/college/ku8s7n9ufecvgpzjnwvv0zwxf8vdmrncmn.png)
Now, substitute this value back into the equation for
 :
:
![\[ 14.7h = 1.575 + 0.1015625 \cdot (8.4)^2 \]](https://img.qammunity.org/2024/formulas/physics/college/ltens8putz2pu0shdo5szf3ftdwmrwdvzn.png)
![\[ 14.7h = 1.575 + 7.57425 \]](https://img.qammunity.org/2024/formulas/physics/college/dykem61t595st3pf4yh84mrsj5l33qa5z6.png)
![\[ 14.7h = 9.14925 \]](https://img.qammunity.org/2024/formulas/physics/college/lzym4i8xgcyefpe00xis0v9t62xf0y9xno.png)
![\[ h \approx 0.623 \ \text{m} \]](https://img.qammunity.org/2024/formulas/physics/college/p04wvbqg8fntzhab8cfs0ya2l4sjljeo70.png)
So, the weight must fall approximately 0.623 meters before it reaches a speed of 2.10 m/s. Now, to find the angular velocity
 of the cylinder:
of the cylinder:
![\[ \omega = (2.10)/(0.25) = 8.4 \ \text{rad/s} \]](https://img.qammunity.org/2024/formulas/physics/college/ku8s7n9ufecvgpzjnwvv0zwxf8vdmrncmn.png)
Therefore, the cylinder is turning at an angular velocity of 8.4 rad/s at this instant.