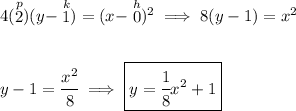Check the picture below.
so as we can see, the focus point is above the directrix, meaning the parabola opens upwards, and since the vertex is halfway between the directrix and focus point, that means the vertex is at (0 , 1), and distance from the vertex to either the focus or directrix is 2, namely p = 2, and is positive since is opening upwards, thus