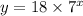Question

Write an exponential function in the form y=ab^x that goes through points (0, 18)and (3, 6174)

Answer 1

`y = 18 * {7}^(x)`

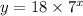
Explanation:

Using the formula for exponential function,

`y = ab {}^(x)`

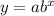
Let plug in 0,18.

`18 = ab {}^(0)`

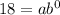
Using the zero power rule,

`b {}^(0) = 1`

`18 = a * 1`

`a = 18`

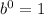
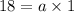
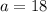
Since a equal 18 let plug in what we know so far

`y = {18b}^(x)`

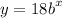
Now let find b.

Let use the other point, 3,6174

`6174 = {18b}^(3)`

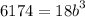
Divide 18 by both sides and we get

`343 = b {}^(3)`

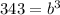
Take the 3rd root of 343

`\sqrt[3]{343} = b = 7`

b=7

The equation is

`y = 18 * 7 {}^(x)`