Question

Five points from a function, f, are plotted in the first quadrant of the coordinte plane as shown

Which equation could represent the function?

A. f(x) = 0.2(1 - 0.1)^x

B. f(x) = 0.2(1 - 0.5)^x

C. f(x) = 0.1(1 - 0.05)^x

D. f(x) = 0.1(1 - 0.25)

Answer 1

The equation that represents the function is:

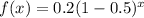`f(x) = 0.2(1 - 0.5)^x`. Option is B.

How to determine the equation that represents the function

To determine the equation that represents the function, analyze the pattern in the given points.

Looking at the y-values, one can observe that each subsequent value is obtained by multiplying the previous value by a constant factor.

Given points:

(0, 0.2), (1, 0.1), (2, 0.05), (3, 0.025), (4, 0.0125)

By analyzing the pattern, it is observed that each y-value is obtained by multiplying the previous value by 0.5 .

Now examine the answer choices:

`A. f(x) = 0.2(1 - 0.1)^x\\B. f(x) = 0.2(1 - 0.5)^x\\C. f(x) = 0.1(1 - 0.05)^x\\D. f(x) = 0.1(1 - 0.25)`

Among the given answer choices, only option B matches the pattern observed.

Now, substitute the x-values into option B and see if it matches the y-values:

For x = 0:

`f(0) = 0.2(1 - 0.5)^0 \\= 0.2(1 - 1)^0`

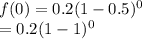
= 0.2(1) = 0.2

For x = 1:

`f(1) = 0.2(1 - 0.5)^1 \\= 0.2(0.5)^1`

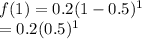
= 0.2(0.5) = 0.1

For x = 2:

`f(2) = 0.2(1 - 0.5)^2 \\= 0.2(0.5)^2`

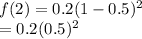
= 0.2(0.25) = 0.05

For x = 3:

`f(3) = 0.2(1 - 0.5)^3\\ = 0.2(0.5)^3`

= 0.2(0.125) = 0.025

For x = 4:

`f(4) = 0.2(1 - 0.5)^4 \\= 0.2(0.5)^4`

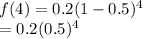
= 0.2(0.0625) = 0.0125

Option B matches all the given points, confirming that it represents the function.

Therefore, the equation that represents the function is:

`f(x) = 0.2(1 - 0.5)^x`

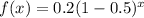
Hence, the correct option is B.