Question

- 4 < - 2x + 9 <= 32​

Answer 1

The solution to the compound inequality, - 4 < - 2x + 9 ≤ 32​ expressed as interval notation is
`((13)/(2), (23)/(2)]`

How solve the compound inequality in interval

To express the solution of the compound inequality in interval, we shall first calculate for x in the expression. This is shown below:

- 4 < - 2x + 9 ≤ 32​

Solving first part, we have:

- 4 < - 2x + 9

Rearrange

2x < 9 + 4

2x < 13

Divide both sides by 2

`x < (13)/(2)`

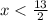
Solving the second part:

- 2x + 9 ≤ 32

Rearrange

-2x ≤ 32 - 9

-2x ≤ 23

Divide both sides by -2

`x\ \le (23)/(-2) \\\\x \ge -(23)/(2)`

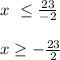
Thus, we can represent the solution to the compound inequality in interval notation as
`((13)/(2), (23)/(2)]`

Complete question:

Solve the compound inequality and express your answer as interval notation

- 4 < - 2x + 9 ≤ 32​