Question

We have = is a family of solutions of the second-order de ′′ = . find a particular solution of the second-order ivp with the given initial conditions. () = − ; ′() = 8 For the given second-order initial value problem (IVP), x(3) = -1 and x′(3) = 8, find a particular solution of the differential equation x′′x = 0.

a. x = 5cos(2) + 3sin(2)
b. x = -3cos(2) + 5sin(2)
c. x = -5cos(2) + 3sin(2)
d. x = 3cos(2) - 5sin(2)

Answer 1

A particular solution of the differential equation x′′x = 0. is
`\( x = -5\cos(2) + 3\sin(2) \)`

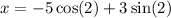
Therefore, correctoption is c.
`\( x = -5\cos(2) + 3\sin(2) \)`

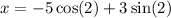
Step-by-step explanation:

To find a particular solution for the second-order initial value problem \(x'' = 0\) with initial conditions \(x(3) = -1\) and \(x'(3) = 8\), we start by integrating the given differential equation twice.

The general solution for x'' = 0 is
`\(x(t) = A\cos(2t) + B\sin(2t)\)`, where A and B are constants. Taking the first and second derivatives, we get
`\(x'(t) = -2A\sin(2t) + 2B\cos(2t)\) and \(x''(t) = -4A\cos(2t) - 4B\sin(2t)\)`.

Now, plug in the initial conditions x(3) = -1 and
`\(x'(3) = 8\)` into the general solution and its derivative. Solve for A and B to obtain the particular solution.

After finding the constants, the particular solution is
`\(x(t) = -5\cos(2t) + 3\sin(2t)\)`.