The line of best fit for the data, obtained using the least squares equation is; y ≈ 1.38·x + 15.68
The option that most closely corresponds to the line of best it is option A
The equation of the line of best can be found as follows;
The possible points on the line obtained from a similar question on the website, presented in tabular form are;
x; -15, -10, -5, 0, 5, 10, 15, 20
y; -4, 2, 7, 16, 22, 30, 37, 43
The line of best fit can be obtained using the least squares regression equation as follows;
y = a + b·x
The formula for the coefficient, b is;
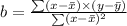
The mean of the x-values,
 = 2.5
= 2.5
Mean of the y-values,
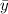 = 19.125
= 19.125
 = 1447.5
= 1447.5
 = 1050
= 1050
Therefore, b is; 1447.5/1050 ≈ 1.38
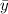 = a + b·
= a + b·

19.125 = a + 1.3786 × 2.5
a = 19.125 - 1.3786 × 2.5
a ≈ 15.68
Therefore, the line of best fit is; y ≈ 1.38·x + 15.68