Question

If ABCABC and DEFDEF are similar triangles with BC=6BC=6, EF=8EF=8, and DF−AC=1DF−AC=1, what is the length of DFDF?

A. 77
B. 99
C. 1010
D. 1111

Answer 1

If ABCABC and DEFDEF are similar triangles with BC=6BC=6, EF=8EF=8, and DF−AC=1DF−AC=1,the length of DFDF is B. 9

Step-by-step explanation:

To find the length of DF, we can use the property of similar triangles. The corresponding sides of similar triangles are proportional.

Let's denote the length of DF as
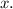`\(x\).` The corresponding sides of ABC and DEF are BC and EF, respectively. Therefore, we can set up the proportion:

`\((BC)/(EF) = (AC)/(DF)\)`

Plug in the given values:
`\((6)/(8) = (AC)/(x)\)`

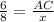
Now, solve for
`\(x\): \(x = (8)/(6) \cdot AC\)`

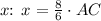
But we know that
`\(DF - AC = 1\),` so
`\(DF = AC + 1\)`

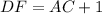
Substitute this into the equation:
`\(x = (8)/(6) \cdot (DF - 1)\)`

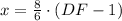
Now, substitute the given values:
`\(9 = (8)/(6) \cdot (DF - 1)\)`

Solve for
`\(DF\): \(DF = (9 \cdot 6)/(8) + 1 = 9\)`

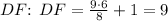
Therefore, the correct answer is B. 9.