Question

The solutions to the equation x² + px + q are x = 5 root , find values of p and q.

Answer 1

To find the values of p and q in the equation x² + px + q = 0, we can use the quadratic formula and substitute the given solutions x = 5 root. Solving for p gives us p = -5, and substituting this back in the equation allows us to solve for q, which is q = 0.75.

Step-by-step explanation:

The equation x² + px + q can be solved using the quadratic formula. For any quadratic equation in the form ax² + bx + c = 0, the solutions can be found using the formula:

`x = (-b \± √(b^2 - 4ac) )/(2a)`

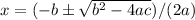
In this case, the equation x² + px + q is in the form of ax² + bx + c = 0, with a = 1, b = p, and c = q. Since the solutions are
`x = 5 √(p)`, we can substitute x with 5 √p in the quadratic formula:

`5 √(p) = (-p \± √(p^2 - 4q) )/2`

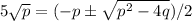
From this equation, we can conclude that p = -5, and substituting this back in the equation we can solve for q:

`5√(-5) = (-(-5) \± √((-5)^2- 4q) )/2`

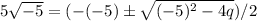
The positive square root gives us
`5 √(5) = (5 + √(25 - 4q)) /2`

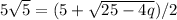
Simplifying further, we get
`5 √(5) = (5 + √(4q + 25)) /2`

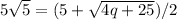
Squaring both sides gives
`25 * 5 = 25 + 5 √(4q + 25)`, which simplifies to 100q = 25 * 10 - 25, and finally q = 75/100 = 0.75.