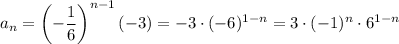Question

This math my life depends on it

Answer 1

A geometric sequence is one in which consecutive terms form a fixed ratio r. In other words, if aₙ is the nth term in the sequence, then

`a_n = a_(n-1)r`

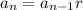
For example, if a₁ = a is the 1st term, then

2nd term = a₂ = a₁r

3rd term = a₃ = a₂r = a₁r²

4th term = a₄ = a₃r = a₁r³

and so on. It's fairly easy to infer that

nth term =
`a_n = a_(n-1)r = a_(n-2)r^2 = a_(n-3)r^3 = \cdots = a_1r^(n-1)`

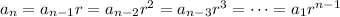
14. We're given the 2nd and 5th terms, a₂ = -243 and a₅ = -9, and we use them to find the ratio r.

a₅ = a₄r = a₃r² = a₂r³

-9 = -243 r³

r³ = 1/27

⇒ r = 1/3

Then the 1st term is

a₁ = a₂/r = -243/(1/3) = -729

and the nth term is recursively given by

`a_n = \frac13a_(n-1)`

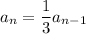
and explicitly by

`a_n = \left(\frac13\right)^(n-1) a_1 = -(729)/(3^(n-1)) = -(3^6)/(3^(n-1)) = -3^(7-n)`

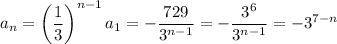
15. Now we have a₄ = 1/72 and a₃ = -1/12. Using what we know about geometric sequences, we have

a₄ / a₃ = (a₃r) / a₃ = r

so that

r = (1/72) / (-1/12) = -1/6

Then the 1st term is

a₁ = a₂/r = a₃/r² = (-1/12) / (-1/6)² = -3

and the nth term is recursively given by

`a_n = -\frac16a_(n-1)`

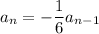
and explicitly by

`a_n = \left(-\frac16\right)^(n-1) (-3) = -3\cdot(-6)^(1-n) = 3\cdot(-1)^n\cdot6^(1-n)`