Question

The current supplied by a battery as a function of time is i(t) = (0.88 a)e-t/(6.0 hr). What is the total number of electrons transported from the positive electrode to the negative electrode from the time the battery is first used until it is essentially dead? (e = 1.60 × 10-19 c).

A) 3.25×10^19 electrons
B) 6.75×10^19 electrons
C) 8.50×10^18 electrons
D) 1.20×10^20 electrons

Answer 1

The total number of electrons transported from the positive electrode to the negative electrode is 6.75 × 10¹⁹ electrons

The answer is option ⇒B

Step-by-step explanation:

To find the total number of electrons transported from the positive electrode to the negative electrode, we need to calculate the charge transported and then convert it to the number of electrons.

Given:

• Current function:
  `i(t) = (0.88 A)e^((-t/(6.0x3.600 s)))`
• Elementary charge:
  `e = 1.60 * 10^-^1^9 C`

To calculate the charge transported, we need to integrate the current function with respect to time from the initial time (when the battery is first used) to the final time (when the battery is dead).

`\int\limits[i(t) dt] = \int\limits[(0.88 A) e^((-t/(6.0x3.600 s)) ) dt]`

To solve this integral, we can use the substitution method. Let's substitute
`u = -t/(6.0x3.600 s)` and
`du = -dt/(6.0x3.600 s)`.

`\int\limits [(0.88 A)e^((-t/(6.0x3.600 s)) ) dt] = -6.0x3.600 s \int\limits[(0.88 A)e^u du]`

Simplifying, we have:

`-6.0x3.600 s \int\limits [(0.88 A)e^u du] = -6.0x3.600 s (0.88 A) \int\limits [e^u du]`

Now, integrating eᵘ with respect to u gives us:

`-6.0x3.600 s (0.88 A) \int\limits [e^u du] = -6.0x3.600 s (0.88 A) e^u`

Substituting back u = -t/(6.0x3.600 s), we get:

`-6.0x3.600 s (0.88 A) e^u = -6.0x3.600 s (0.88 A) e^((-t/(6.0x3.600 s) ))`

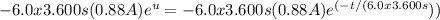
Now, we evaluate this expression from the initial time (t=0) to the final time (t=∞) when the battery is essentially dead.

Using the limits of integration, the charge transported is:

Charge transported = -6.0x3.600 s (0.88 A) e⁽⁻∞/⁽⁶ˣ³⁶⁰⁰ ˢ⁾) - (-6.0x3.600 s (0.88 A) e⁽⁰/⁽⁶ˣ³⁶⁰⁰ ˢ⁾))

Since e⁽⁻∞⁾ approaches 0 and e⁰= 1, the expression simplifies to:

Charge transported = 6.0x3.600 s (0.88 A)

Finally, we convert the charge transported to the number of electrons using the elementary charge:

Number of electrons = Charge transported / elementary charge

Substituting the values:

Number of electrons = (6.0x3.600 s (0.88 A)) / (1.60 × 10⁻¹⁹ C)

Calculating this expression gives us:

Number of electrons ≈ 6.75 × 10¹⁹ electrons

Therefore, the correct answer is option B) 6.75 × 10¹⁹ electrons.