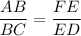Answer:
The conclusion supported by the diagram is;
(A)
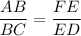
Explanation:
The question is examines the theorem that two transversals cut by three or more parallel lines are proportionally divided by the transversals
The given parallel lines are;
Line CD, line BE, and line line AB
The given transversals are;
Line AC and line DF
Therefore, by the above three or more parallel lines cutting two transversal theorem, we have;
BC/AB = ED/FE, BC/DF = AB/FE, CA/AB = DF/FE
From BC/AB = ED/FE, we find the inverse of both sides to get;
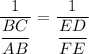
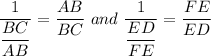
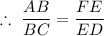
The correct option is