Question

Write a polynomial of 3rd degree with the given real or complex roots. Express your answer in standard form.

A) f(x) = x^3 - 3x^2 - 2x
B) f(x) = x^3 - 2x^2 - x
C) f(x) = x^3 - 3x^2 + 2x
D) f(x) = x^3 - 2x^2 + x

Answer 1

To determine the polynomial with the given roots, we solve the equation using the quadratic formula and compare the options.

Step-by-step explanation:

The given options are:

A)
`f(x) = x^3 - 3x^2 - 2x`

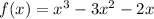
B)
`f(x) = x^3 - 2x^2 - x`

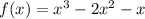
C)
`f(x) = x^3 - 3x^2 + 2x`

D)
`f(x) = x^3 - 2x^2 + x`

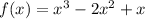
To determine which polynomial has the given roots, we need to solve the equation
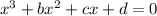`x^3 + bx^2 + cx + d = 0` using the quadratic formula. The roots of the polynomial are the values of x that make the equation equal to zero. Comparing the given options with the quadratic formula, we find that option C)
`f(x) = x^3 - 3x^2 + 2x` has the same roots as the given equation.