Question

A 58.0 g sample of water vapor is condensing at 100.0 °C. Over time, all the water vapor is converted to liquid water at a temperature of 58 °C.

Answer 1

The total heat released during the process of condensing 58.0 g of water vapor at 100.0 °C to liquid water at 58.0 °C is approximately 131.244 kJ.

How to find total heat?

To calculate the total heat released during the process of condensing water vapor to liquid water, we can use the formula:

`\[ Q = m \cdot \Delta H \]`

where:

Q = heat released,

m = mass of the substance (water in this case),

ΔH = enthalpy change for the phase transition.

For the condensation of water vapor to liquid water, the enthalpy change (ΔH) is the heat of vaporization (
`\( \Delta H_{\text{vap}} \)`).

Given:

Mass of water vapor (m) = 58.0 g

Heat of vaporization (
`\( \Delta H_{\text{vap}} \)`) for water at 100 °C =
`\( 40.79 \, \text{kJ/mol} \)`

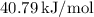
First, find the moles of water vapor using the molar mass of water (
`\( H_2O \)`):

`\[ \text{Molar mass of } H_2O = 18.015 \, \text{g/mol} \]`

`\[ \text{Moles of } H_2O = \frac{\text{Mass}}{\text{Molar mass}} = \frac{58.0 \, \text{g}}{18.015 \, \text{g/mol}} \]`

Now, calculate the heat released:

`\[ Q = \text{Moles} * \Delta H_{\text{vap}} \]`

`\[ Q = \left(\frac{58.0 \, \text{g}}{18.015 \, \text{g/mol}}\right) * (40.79 \, \text{kJ/mol}) \]`

`\[ Q = \text{Moles} * \Delta H_{\text{vap}} \]`

`\[ Q = (3.218 \, \text{mol}) * (40.79 \, \text{kJ/mol}) \]`

`\[ Q \approx 131.244 \, \text{kJ} \]`

So, the total heat released during the process of condensing 58.0 g of water vapor at 100.0 °C to liquid water at 58.0 °C is approximately 131.244 kJ.

Complete question:

A 58.0 g sample of water vapor is condensing at 100.0 °C. Over time, all the water vapor is converted to liquid water at a temperature of 58 °C. Calculate the total heat released during this process.