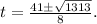The values of t for which the rocket's height is 92 feet are approximately:
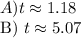
To find the values of t for which the rocket's height is 92 feet, we need to solve the equation
 when h is equal to 92.
when h is equal to 92.
So, we can write the equation as

To solve this quadratic equation, we can rearrange it to
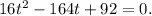
Now, we can factorize or use the quadratic formula to find the values of t.
Using the quadratic formula, which states that for an equation of the form
 , the solutions for x are given by
, the solutions for x are given by
 , we can find the values of t.
, we can find the values of t.
For our equation, a = 16, b = -164, and c = 92.
Substituting these values into the quadratic formula, we have:
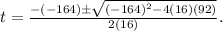
Simplifying the expression inside the square root, we get:
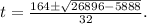
Further simplifying, we have:
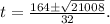
Now, we can simplify the square root:
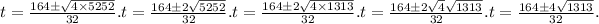
Simplifying further, we have: