Question

For the last decade, the number of insured children who had dental cleanings has been growing by 5% per year or by about 68 children per year, depending on how the growth is modeled. This year, 1760 insured children have dental cleanings. To the nearest whole number, what is the difference between the numbers of children that the models predict will have dental cleanings 3 years from now?

(A) 9
(B) 10
(C) 11
(D) 12

Answer 1

The percentage growth model predicts approximately 2038 children, while the linear growth model predicts 1964 children in 3 years. The difference between these models is approximately 74 children, not matching the options provided.

Step-by-step explanation:

To solve for the difference in the number of insured children predicted to have dental cleanings in 3 years, as per the two different models of growth, we need to calculate the predictions separately for each model and then find the difference.

Using the percentage growth model, the number of children with cleanings in 3 years (N) can be found using the formula
`N = P(1+r)^t`, where P is the present number, r is the growth rate (as a decimal), and t is the time in years. Therefore:

`N = 1760(1+0.05)^3`

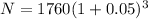
N ≈ 2038 children

Using the linear growth model, we simply add 68 children per year. After 3 years:

N = 1760 + 68(3)

N = 1964 children

Finally, the difference between these two models:

Difference = 2038 - 1964 ≈ 74 children

Therefore, the correct answer is not among the options provided.