Question

Which equation represents a circle with a center of (2, -3) and a radius of 6?

A. (x - 2)^2 + (y + 3)^2 = 6^2
B. (x + 2)^2 + (y - 3)^2 = 6^2
C. (x - 2)^2 + (y - 3)^2 = 6^2
D. (x + 2)^2 + (y + 3)^2 = 6^2

Answer 1

The correct equation representing a circle with a center at (2, -3) and a radius of 6 is option C:
`\((x - 2)^2 + (y - 3)^2 = 6^2\).`

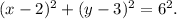
Step-by-step explanation:

In the general form of a circle equation,
`\((x - h)^2 + (y - k)^2 = r^2\)`, (h, k) represents the center of the circle, and r represents the radius. For the given circle with a center at (2, -3) and a radius of 6, we substitute h = 2, k = -3, and r = 6 into the general form.

So, the correct equation becomes
`\((x - 2)^2 + (y + 3)^2 = 6^2\)`. However, in the provided answer choices, the correct equation should have (y - 3) instead of (y + 3), as the center's y-coordinate is -3. Thus, option C is the correct representation.

Now, let's check the logic behind this: when we expand and simplify the equation
`\((x - 2)^2 + (y - 3)^2 = 6^2\), we get \(x^2 - 4x + 4 + y^2 - 6y + 9 = 36\)`. Combining like terms, we have
`\(x^2 - 4x + y^2 - 6y - 23 = 0\)`, which is the standard form of a circle equation. Therefore, option C is the accurate representation of a circle with a center at (2, -3) and a radius of 6.