Question

The half-life of a certain radioactive material is 42 days. An initial amount of the material has a mass of 49 kg. Write an exponential function that models the decay of this material. Find how much radioactive material remains after 8 days. Round your answer to the nearest thousandth.

A. y = 49(1/2)^(42x); 0kg
B. y = 1/2(1/49)^(1/42x); 0.238kg
C. y = 49(1/2)^(1/42x); 42.940kg
D. y = 2(1/49)^(1/42x); 0.953kg

Answer 1

The exponential function that models the decay of the material is
`y = 42((1)/(2))^{(1)/(42)x` and the amount remaining after 8 days is 42.940 Kg (option C)

How to determine the function and amount after 8 days?

The exponential function that models the decay of the material can be determined as shown below:

• Half-life of radioactive material (t½) = 42 days
• Time (t) = x
• Initial amount (y₀) = 49 Kg
• Exponential function = Amount remaining after time x (y) =?

`y = y_0\ *\ ((1)/(2))^{(t)/(t_(1/2))} \\\\y = 49\ *\ ((1)/(2))^{(x)/(42)}\\\\y = 49 ((1)/(2))^{(1)/(42)x}`

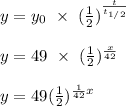
Finally, we shall obtain the amount remaining after 8 days. This is sshown below:

• Half-life of radioactive material (t½) = 42 days
• Time (t) = 8 days
• Initial amount (y₀) = 49 Kg
• Amount remaining after 8 days (y) =?

`y = y_0\ *\ ((1)/(2))^{(t)/(t_(1/2))} \\\\y = 49\ *\ ((1)/(2))^{(8)/(42)}\\\\y = 42.940\ Kg`

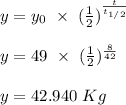
From the above calculation, we can conclude that the correct answer is option C