Final answer:
The equation of this circle is
 .
.
Step-by-step explanation:
The equation of a circle centered at point (h, k) with radius r is given by:
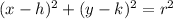
In this case, the center of the circle is at (0, -10) and the radius is 10 units. Substituting the values into the equation, we get:

Simplifying further, we have:

Therefore, the equation of this circle is
 , which corresponds to option C.
, which corresponds to option C.