Question

Present in a complex form (general and exponential form), and draw in a complex plane the voltage, as well as the vector -phasor of the voltage, whose current value is u (t) = 212.13 ∙ sin (ω ∙ t - 63˚) v​.

Answer 1

The voltage, presented in a complex form, is given by
`\( V(t) = 212.13 \cdot e^(j(\omega t - 63^\circ)) \)` V, where ( j ) is the imaginary unit. The corresponding vector-phaser in the complex plane for the voltage is also depicted.

Step-by-step explanation:

To express the voltage in a complex form, we utilize Euler's formula, which states that
`\( e^(j\theta) = \cos(\theta) + j\sin(\theta) \).`The given current function is
`\( u(t) = 212.13 \cdot \sin(\omega t - 63^\circ) \)` V. To find the voltage, we need to multiply this by the complex impedance, ( Z ), which is equal to the magnitude of the impedance times
`\( e^(j\phi) \)`, where
`\( \phi \)` is the phase angle. In this case,
`\( Z = 212.13 \cdot e^(-j63^\circ) \).` Therefore, the voltage is given by
`\( V(t) = u(t) \cdot Z \).`Substituting in the given values and simplifying, we obtain
`\( V(t) = 212.13 \cdot e^(j(\omega t - 63^\circ)) \) V.`

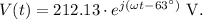
Now, to illustrate this in the complex plane, we plot the real and imaginary parts of the voltage as vectors. The real part corresponds to the cosine term, and the imaginary part corresponds to the sine term. The angle
`\( -63^\circ \)` represents the phase shift in the complex plane. The resulting vector-phaser represents the voltage in both magnitude and phase.