Question

Use synthetic division and the given factor to completely factor the polynomial function x^3 + 6x^2 + 3x - 10: x + 5.

A. x^2 + x - 2
B. x^2 - x - 2
C. x^2 + x + 2
D. x^2 - x + 2

Answer 1

B.
`x^2 - x - 2` because The polynomial
`x^3 + 6x^2 + 3x - 10 completely factors as (x + 5)(x^2 - x - 2)`, determined through synthetic division and further factoring the quadratic term.

Step-by-step explanation:

To factor the given polynomial using synthetic division, we first set the divisor, x + 5, equal to zero to find the root: x + 5 = 0, which gives x = -5. Using synthetic division, we divide the polynomial by x + 5, resulting in the quotient x^2 - x - 2. This means that
`(x + 5)(x^2 - x - 2)` is the completely factored form.

The factorization process involves dividing the original polynomial by its root (x + 5) using synthetic division, leaving us with a quadratic quotient,
`x^2 - x - 2`. This quadratic factor can be further factored as (x - 2)(x + 1). Therefore, the final factored form is (x + 5)(x - 2)(x + 1), which can be rearranged as
`(x + 5)(x^2 - x - 2).`

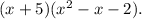
In summary, by identifying the root using synthetic division and factoring the resulting quadratic expression, we find that the completely factored form of the given polynomial is (x + 5)(x^2 - x - 2).