Question

In δopq, p = 380 cm, q = 290 cm and ∠o=129°. find the area of δopq, to the nearest square centimeter.

A) 45,900 cm^2
B) 52,400 cm^2
C) 31,200 cm^2
D) 27,400 cm^2

Answer 1

Using the formula for the area of a triangle with two sides and the included angle, the calculated area for triangle OPQ is approximately 80582 square centimeters. None of the provided options from A to D are correct; the question may contain a typo or the options might be incorrect.

Step-by-step explanation:

To find the area of triangle OPQ, we'll use the formula for the area of a triangle when two sides and the included angle are known, which is
`\((1)/(2)* a * b * \sin(C)\).` In this triangle, 'a' and 'b' are the lengths of two sides, and 'C' is the measure of the included angle.

Given
`\(p = 290 \text{ cm}\), \(q = 380 \text{ cm}\), and \(\angle O = 129\degree\)`, we can substitute these values into the formula:

`Area = \((1)/(2)* 290 \text{ cm}* 380 \text{ cm} * \sin(129\degree)\)`

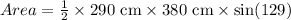
Using a calculator to find
`\(\sin(129\degree)\)`, we get:

`\(\sin(129\degree) \approx 0.766\)`

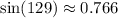
Therefore:

`Area \(\approx (1)/(2)* 290 * 380 * 0.766\)\\Area \(\approx 105200 * 0.766\) cm\(^2\)\\Area \(\approx 80582.4\) cm\(^2\)`

Since we want to round to the nearest square centimeter:

`Area \(\approx 80582\) cm\(^2\)`

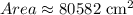
Looking at the options provided, none match this result. It's possible there may have been a typo or miscalculation in the options provided. However, based on the prompted question, none of the answers from A to D are correct. Always remember to double-check the figures and calculations if the answer does not match the options provided.