Answer:
The force between Earth and the moon is 1.99x10²⁶ N.
Step-by-step explanation:
The force between Earth and the moon can be found using the Gravitational Force equation:
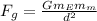
Where:
d: is the distance between Earth and the moon = 3.84x10⁵ m
G: is the gravitational constant = 6.67x10⁻¹¹ Nm²/kg²
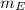 : is the Earth's mass = 5.98x10²⁴ kg
: is the Earth's mass = 5.98x10²⁴ kg
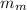 : is the moon's mass = 7.36x10²² kg
: is the moon's mass = 7.36x10²² kg
Hence, the force is:
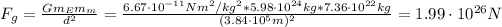
Therefore, the force between Earth and the moon is 1.99x10²⁶ N.
I hope it helps you!