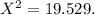Question

A doctor’s surgery assumes that about 10% of their patients will come in with emergencies, 40% with non-emergencies, and 50% with general questions. One day a doctor sees 15 emergencies, 20 non-emergencies and 19 patients with general questions. Calculate the Chi-square goodness of fit value.

Answer 1

The chi-square goodness-of-fit value is approximately
`\(X^2 = 19.529\).`

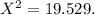
The chi-square goodness-of-fit test is used to determine whether there is a significant difference between the expected and observed frequencies in a categorical distribution. The formula for the chi-square goodness-of-fit test statistic
`(\(X^2\))` is:

`\[ X^2 = \sum \frac{{(O_i - E_i)^2}}{{E_i}} \]`

where:

-
`\(O_i\)` is the observed frequency for category i,

-
`\(E_i\)` is the expected frequency for category i, and

- The sum is taken over all categories.

In this case, the categories are emergencies, non-emergencies, and general questions. Let's calculate
`\(X^2\)`using the provided data:

1. **Define the observed frequencies
`(\(O_i\))`:

- Emergencies
`(\(O_1\))`: 15

- Non-emergencies
`(\(O_2\))`: 20

- General questions
`(\(O_3\))`: 19

2. **Calculate the expected frequencies
`(\(E_i\))`:**

- Expected emergencies
`(\(E_1\))`:
`\(0.10 * (15 + 20 + 19)\)`

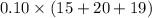
- Expected non-emergencies
`(\(E_2\))`:
`\(0.40 * (15 + 20 + 19)\)`

- Expected general questions
`(\(E_3\))`:
`\(0.50 * (15 + 20 + 19)\)`

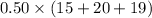
3. **Plug the values into the chi-square formula and calculate:**

`\[ X^2 = \frac{{(15 - E_1)^2}}{{E_1}} + \frac{{(20 - E_2)^2}}{{E_2}} + \frac{{(19 - E_3)^2}}{{E_3}} \]`

Let's perform these calculations.

1. **Define the observed frequencies
`(\(O_i\))`:**

`- \(O_1\): 15 (Emergencies)\\ - \(O_2\): 20 (Non-emergencies)\\ - \(O_3\): 19 (General questions)`

2. **Calculate the expected frequencies
`(\(E_i\))`:**

`- \(E_1\): \(0.10 * (15 + 20 + 19) = 5.4\)\\ - \(E_2\): \(0.40 * (15 + 20 + 19) = 21.6\)\\ - \(E_3\): \(0.50 * (15 + 20 + 19) = 27\)`

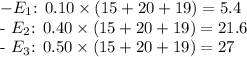
3. **Plug the values into the chi-square formula and calculate:**

`\[ X^2 = \frac{{(15 - 5.4)^2}}{{5.4}} + \frac{{(20 - 21.6)^2}}{{21.6}} + \frac{{(19 - 27)^2}}{{27}} \]`

Now, compute the values and sum them up to get the chi-square statistic.

`\[ X^2 = \frac{{(15 - 5.4)^2}}{{5.4}} + \frac{{(20 - 21.6)^2}}{{21.6}} + \frac{{(19 - 27)^2}}{{27}} \]\\X^2 = \frac{{(9.6)^2}}{{5.4}} + \frac{{(-1.6)^2}}{{21.6}} + \frac{{(-8)^2}}{{27}} \]\\ X^2 = \frac{{92.16}}{{5.4}} + \frac{{2.56}}{{21.6}} + \frac{{64}}{{27}} \]\\ X^2 \approx 17.04 + 0.1185 + 2.3704 \]\\ X^2 \approx 19.529 \]`

Therefore, the chi-square goodness-of-fit value is approximately
`\(X^2 = 19.529\).`