Question

A right triangle is removed from a rectangle to create the shaded region shown below. Find the area of the shaded region. Be sure to include the correct unit in your answer. Explanation 6ft Check 9ft 4 2ft 3ft 0 8 08 ft X ft² ft³ ? E

Answer 1

51 ft²

Step-by-step explanation

To find the area of the shaded region, we have to find the area of the entire rectangle and then, subtract the area of the right triangle that was removed.

The dimensions of the rectangle are 6 ft and 9 ft, so its area is,

`A_(rectangle)=6ft*9ft=54ft^2`

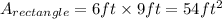
The base and height of the removed triangle are 2 ft and 3 ft long, so the area is,

`A_(triangle)=(2ft*3ft)/(2)=3ft^2`

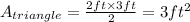
So, the area of the shaded region is,

`A_(region)=A_(rectangle)-A_(triangle)=54ft^2-3ft^2=51ft^2`

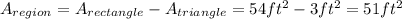
Hence, the area of the shaded region is 51 ft².