ANSWER
51 ft²
Step-by-step explanation
To find the area of the shaded region, we have to find the area of the entire rectangle and then, subtract the area of the right triangle that was removed.
The dimensions of the rectangle are 6 ft and 9 ft, so its area is,
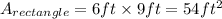
The base and height of the removed triangle are 2 ft and 3 ft long, so the area is,
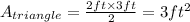
So, the area of the shaded region is,
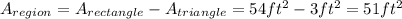
Hence, the area of the shaded region is 51 ft².