Final Answer:
The triangle QRT formed by the coordinates Q(-2, -1), R(1, 5), and T(-8, -4) is classified as a scalene triangle.
Step-by-step explanation:
To determine the classification of the triangle by its sides, we need to calculate the lengths of its three sides using the distance formula:
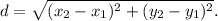
1. Calculating the length of side QR:
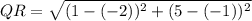
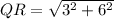
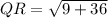
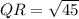
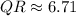
2. Calculating the length of side RT:

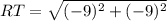
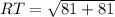
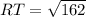
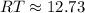
3. Calculating the length of side QT:
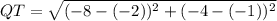

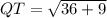
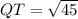

Upon calculation, the lengths of the sides are approximately 6.71, 12.73, and 6.71 units. As none of the side lengths are equal, the triangle QRT is classified as a scalene triangle. This classification indicates that no two sides of the triangle are of equal length.