Question

Two numbers differ by 7.If their product is 120, find the number

Answer 1

Two numbers differ by 7.If their product is 120, find the number​

Let

x and y the numbers

we have

x-y=7 ------> x=7+y -----> equation A

x*y=120 ----> equation B

solve the system

substitute equation A in equation B

(7+y)*y=120

solve for y

y^2+7y-120=0

solve the quadratic equation by graphing

the solutions are

y=8 and y=-15

Find out the value of x

For y=8

x=7+8=15

For y=-15

x=7+(-15)

x=-8

therefore

the numbers are

8 and 15 or -8 and -15

Problem N 2

we have that

EF=9 cm ----> given

EF=EH+HF ----> by addition segment postulate

substitute given values

9=x+HF

HF=(9-x) cm

step 1

In the right triangle EDH

Applying the Pythagorean Theorem

ED^2=EH^2+DH^2-----> DH^2=ED^2-EH^2

DH^2=(x+3)^2-x^2 ------> equation A

step 2

In the right triangle DHF

Applying the Pythagorean Theorem

DF^2=HF^2+DH^2 -----> DH^2=DF^2-HF^2

DH^2=(2x)^2-(9-x)^2 ------> equation B

step 3

equate equation A and equation B

`\mleft(x+3\mright)^2-x^2=(2x)^2-\mleft(9-x\mright)^2`

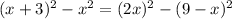
Simplify

x^2+6x+9-x^2=4x^2-(81-18x+x^2)

6x+9=4x^2-81+18x-x^2

6x+9=3x^2+18x-81

3x^2+18x-81-6x-9=0

3x^2+12x-90=0 -------> quadratic equation

step 4

Solve for x

Complete the square

3x^2+12x=90

Factor 3

3(x^2+4x)=90

simplify

(x^2+4x)=30

x^2+4x+4=30+4

rewrite as perfect squares

(x+2)^2=34

`(x+2)^2=34`

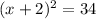
take the square root both sides

`\begin{gathered} x+2=\pm\sqrt[]{34} \\ x=-2\pm\sqrt[]{34} \end{gathered}`

The value of x must be a positive value

therefore

`\begin{gathered} x=-2+\sqrt[]{34} \\ x=3.83\text{ cm} \end{gathered}`