Let x be the number of miles and y the total cost of the service.
Since the company They Haul charges $40 plus 0.20 per mile, then for x miles they would charge $40 plus 0.2x:
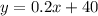
Since the company Good Deal charges $80 regardless of the number of miles, then:
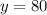
To find the intersection of both equations, set both expressions to be equal and solve for x:

Then, the cost is the same for both companies if the amount of miles is equal to 200, and the cost would be $80.
To find the y-intercept for the company They Haul, evaluate the expression for x=0:
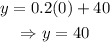
Since the expression for Good Deal does not depend on the value of x, then the y-intercept is:
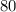
To graph the equations:
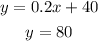
Find two points on each line and draw a line through those points.
To find a point on a line, substitute different values of x to find the corresponding values of y.
For instance, choose x=0 and x=100. From the first equation, we obtain the following values for y:

Then, the points (0,40) and (100,60) belong to the first line. Plot those two points on a coordinate plane and then draw a line through those points:
For the other line, the value of y is always 80 regardless of the value of x. Then, the points (50,80) and (150,80) belong to the line. Do the same procedure to draw that second line:
We can see that They Haul (red) charges more than Good Deal whenever the number of miles is greater than 200.
The slope-intercept form of the equation of a line with slope m and y-intercept b is:

We already knew the equations for They Haul and Good Deal:
They Haul:
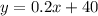
The slope is equal to 0.2
Good Deal:
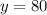
Since the x-variable does not appear, than means that the coefficient of x is 0, so the slope is equal to 0.