Answer:
x= -1 and y= -1
Explanation:
Power through with me as I explain this, its a bit long of an explanation.
To solve the following system of equations, we need to write 5x-4y=-1 in slope-intercept form.
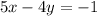
Subtract 5x from both sides.


Divide each term by -4.

Remember that dividing two negative values results in a positive value.

Reorder the terms. (Reordering terms makes the work tidier, it does not change the result)
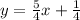
Now that we have the slope-intercept form, we can solve by subsitution with the two equations to find the solution.
Substitute
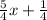 for y in
for y in
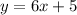 .
.
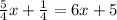
Subtract 1/4 from each side.
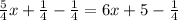
Simplify the left side.
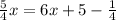
Simplify the right side.

Subtract 6x from both sides.
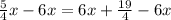
Simplify.
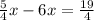
Simplify the left side of the equation by factoring out x.
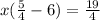
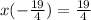
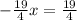
Multiply each side by 4.
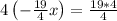
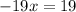
Divide both side by 19.


Now that we know the value of x, we need to find y.
Insert the value of x in the equation y= 6x+5
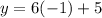
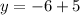
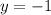
Thus, x= -1 and y= -1 OR (-1,-1)