Final Answer:
a) The common difference (\(d\)) is -6.
b) The first term (\(a\)) is 120.
c) The sum of the first \(n\) terms
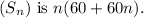
d) The possible values of \(n\) are 10 and -20.
Step-by-step explanation:
a) In an arithmetic series, the n-th term is given by
 , where \(a\) is the first term and \(d\) is the common difference. Given \(a_3 = 108\) and \(a_{12} = 54\), we can set up equations to solve for \(d\), which results in \(d = -6\).
, where \(a\) is the first term and \(d\) is the common difference. Given \(a_3 = 108\) and \(a_{12} = 54\), we can set up equations to solve for \(d\), which results in \(d = -6\).
b) Once \(d\) is known, we can find the first term \(a\) using the formula
 , with
, with
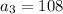 . Solving for \(a\), we get a = 120.
. Solving for \(a\), we get a = 120.
c) The sum of the first
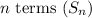 of an arithmetic series is given by
of an arithmetic series is given by
![\(S_n = (n)/(2)[2a + (n-1)d]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/zd8td9bvltqmdg55dvue7b0t8kaquggz2q.png) . Substituting the known values a = 120and d = -6, we obtain
. Substituting the known values a = 120and d = -6, we obtain
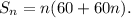
d) To find the possible values of n given
 , we set the expression for
, we set the expression for
 equal to 1200 and solve for n , resulting in the possible values n = 10 and n = -20.
equal to 1200 and solve for n , resulting in the possible values n = 10 and n = -20.