Question

A pitcher throws an overhand fastball from an approximate height of 2.65 m and at an angle of 2.5° below horizontal. The catcher catches the ball high in the strike zone, at a height of 1.02 m above the ground. If the pitcher's mound and home plate are 18.5 m apart, what is the initial velocity of the pitch?

Answer 1

The initial velocity of the pitch is approximately 36.5 m/s

Step-by-step explanation:

The given parameters of the thrown fastball are;

The height at which the pitcher throws the fastball, h₁ = 2.65 m

The angle direction in which the ball is thrown, θ = 2.5° below the horizontal

The height above the ground the catcher catches the ball, h₂ = 1.02 m

The distance between the pitcher's mound and the home plate = 18.5 m

Let 'u' represent the initial velocity of the pitch

From h =
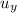`u_y`·t + 1/2·g·t², we have;

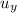`u_y` = The vertical velocity = u·sin(θ) = u·sin(2.5°)

h = 2.65 m - 1.02 m = 1.63 m

uₓ·t = u·cos(θ) = u·cos(2.5°) × t = 18.5 m

∴ t = 18.5 m/(u·cos(2.5°))

∴ h =
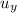`u_y`·t + 1/2·g·t² = (u·sin(2.5°))×(18.5/(u·cos(2.5°))) + 1/2·g·t²

1.63 = 8.5·tan(2.5°) + 1/2 × 9.8 × t²

t² = (1.63 - 8.5·tan(2.5°))/(1/2 × 9.8) = 0.25691469087

t = √(0.25691469087) ≈ 0.50686752763

t ≈ 0.50686752763 seconds

u = 18.5 m/(t·cos(2.5°)) = 18.5 m/(0.50686752763 s × cos(2.5°)) = 36.5334603 m/s ≈ 36.5 m/s

The initial velocity of the pitch = u ≈ 36.5 m/s.