Question

Paige knows that a certain shape is a rectangle. She has found the slope of one side to be 2/3. What is the slope of the opposite side? What are the slopes of theother two sides?opposite side: 2/3other sides:-3opposite side: 2/3other sides:-2/3opposite side: 2/3other sides: -3/2opposite side: -3/2other sides: 2/3

Answer 1

Since the shape is a rectangle, the slope of the opposite side include the following:

D. opposite side: -3/2

other sides: 2/3.

In Mathematics and Euclidean Geometry, a rectangle refers to a type of quadrilateral or polygon in which its opposite sides are equal and all the angles that are formed are right angles, measuring 90 degrees.

Perpendicular lines refers to two (2) lines that intersect or meet each other at an angle of 90° (right angles).

For two lines to be perpendicular, the product of their slopes (m) must be -1 or a negative reciprocal of each other;

`m_1 * m_2=-1`

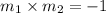
slope of opposite side × slope of other side = -1

slope of opposite side × 2/3 = -1

slope of opposite side = -3/2

Answer 2

A rectangle consists of two pairs of parallel segments such that two of them (which are parallel to each other) are perpendicular to the remaining two segments.

Then, in our case, the slope of two of the sides of the rectangle is 2/3, those two sides are opposite to each other (a rectangle is a parallelogram); therefore,

What is the slope of the opposite side? The answer is 2/3

On the other hand, the two remaining sides have to be perpendicular to the side whose slope is equal to 2/3. The slope of two perpendicular lines has the next property

`m_1\cdot m_2=-1`

Then,

`\begin{gathered} (2)/(3)\cdot m_2=-1 \\ \Rightarrow m_2=-(3)/(2) \end{gathered}`

Thus,

What are the slopes of the two remaining sides? The answer is -3/2

Option C is the answer