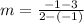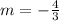Answer
• The instantaneous rate of change at x= – 1 is 0 (zero).
• The average rate of change on the interval -1 ≤ x ≤ 2 is –4/3.
Step-by-step explanation
The instantaneous rate of change is the derivative at the point given. In our case, when x = –1, it is a maximum point and the tangent to this line is a constant y = –3 (tangent line represented by the blue line in the figure given). Thus, the derivative is 0, resulting in an instantaneous rate of change of 0:
Contrarily, the average rate of change on the interval –1 ≤ X ≤ 2 is the slope of the tangent line between points x = –1 and x = –2 (represented by the red line in the figure given), then, the slope can be calculated using the following formula:

Then, to use this formula we have to find the coordinates of these points:
Thus, the coordinates are (–1, 3) and (2, –1), by replacing these values we get: