Answer:
sin(α + β) = -84/205
tan(α + β) = 84/187
Step-by-step explanation:
To find sin(α + β), we will use the following identity
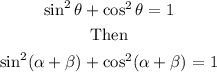
So, solving for sin(α + β), we get:
![\sin (\alpha+\beta)=\pm_{}\sqrt[]{1-\cos^2(\alpha+\beta)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/r5mwi5jplb1avu99tbvn.png)
Now, we can replace cos(α + β) = -187/205 to get:
![\begin{gathered} \sin (\alpha+\beta)=\pm\sqrt[]{1-((187)/(205))^2} \\ \sin (\alpha+\beta)=\pm(84)/(205) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/j6ch1325k23va13238jw.png)
Then, α + β is on quadrant III. It means that the sine of the angle is negative. Therefore
sin(α + β) = -84/205
Finally, to add tan(α + β), we will use the following
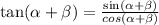
Replacing the values, we get:
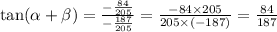
Therefore
tan(α + β) = 84/187