Hello!
We have the equation:
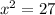
The first thing to solve it is to calculate the square root of each side, look:
![\begin{gathered} \sqrt[]{x^2}=\sqrt[]{27} \\ x=\sqrt[]{27} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/bwzdsvsup0b435iwwduq.png)
Let's calculate this square root by factorization:
![\sqrt[]{27}=+-3\sqrt[]{3}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/c7zpjoug7w195rmycs60.png)
Remember that when we talk about square roots, we must remember that we have two possible values: the positive and the negative. So, x will have two solutions, look:
![\begin{gathered} x_1=3\sqrt[]{3} \\ \\ x_2=-3\sqrt[]{3} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9pdbkvjhztwr4qkg5rk6.png)
Answering your question, this equation has two solutions.