Final answer:
After 10 years, by depositing $18,000 in a bank account with a 5% interest rate compounded continuously, you will have approximately $29,676.96.
Step-by-step explanation:
To calculate the amount of money you will have in a bank after 10 years if you deposit $18,000 into a savings account with a 5% interest rate compounded continuously, you use the formula for continuous compounding interest, which is A =
 , where:
, where:
- P is the principal amount (the initial amount of money)
- r is the annual interest rate (in decimal form)
- t is the time the money is invested for
- e is the base of the natural logarithm (approximately equal to 2.71828)
- A is the amount of money accumulated after n years, including interest.
For this scenario:
- P = $18,000
- r = 0.05 (5% as a decimal)
- t = 10 years
Substituting these values into the formula gives us:
A =
 = 18000 *
= 18000 *
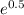
Using a calculator to find
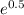 , we get:
, we get:
A = 18000 * 1.64872 (approximately)
A = $29,676.96
Therefore, after 10 years, you will have approximately $29,676.96 in the bank account. This amount is rounded to the nearest cent as requested.